Major Qualifying Project
The Major Qualifying Project (MQP) is a professional-level design or research experience completed by every WPI undergraduate. An integral element of WPI's project-based education, the immersive capstone project enables students to synthesize their learning by tackling and solving real-world problems in their fields of study.
MQPs completed by Actuarial Mathematics (MAC) and Mathematical Sciences (MA) students:
Actuarial Mathematics
Title: Copula Modeling: An Application to Workers’ Compensation Claims
Students: Alison Lambert, Donovan Robillard, Lexi Ferrini
Advisors: Jon Abraham, Barry Posterro
Sponsor: Hanover Insurance Group
Academic Year: 2021-2022
Copulas are multivariate probability distributions used in the modeling of multiple random variables. In insurance, they are used to create models that preserve the relationship between a claim’s loss amount and any associated expenses, especially in large loss scenarios. The goal of this project was to develop a copula model for losses and their associated expenses and determine whether their use produces different results than current modeling methods. Through data analysis and simulation, the team identified that a copula model could be applied to claims in Workers’ Compensation. It was found that the copula model did not produce significantly different results than those produced using the sponsor’s traditional methods, validating their current models.
Title: Trends in Health Reserves
Students: Danielle Rubin and Bianca Amarasekera
Advisors: Jon Abraham, Barry Posterro
Sponsor: Milliman
Academic Year: 2020-2021
This paper evaluates reserving trends in the health insurance industry. Our analysis used 2016 to 2019 data from Annual Health Statements and includes 1,749 distinct health companies and subsidiaries in Medical, Medicare, Medicaid, and the Total of lines of business. We created and examined various distributions that describe the accuracy and conservativeness of the industry. Also, we analyzed how past reserving trends relate to future trends and identified various attributes that are correlated with reserve estimates. Lastly, using our analysis and 2016 to 2018 data, we created a model to forecast future reserve adequacy. We tested the model by predicting 2019 reserve accuracy and comparing it to the actual 2019 data.
Analysis
Title: Unique and Stable Determination of a Crack in a Half Space Governed by Laplace’s Equation
Student: Karl Ramus (MA)
Advisor: Darko Volkov
Academic Year: 2024-2025
In this paper, we consider a solution to Laplace’s equation in a specific domain; namely, a half space with a crack. This crack is represented as a line segment below the x-axis, across which there is a jump in function value. This jump itself varies along the crack, but is assumed to be fully supported over the crack, as otherwise there would effectively be no crack. The question we seek to solve: given some measurements of our function along the boundary- i.e. along a subset of the x-axis, can we uniquely determine the location of the crack? The answer to this turns out to be yes. In addition, we prove that the error in this determination is linearly bounded above. In more mathematical language, the determination of the crack is proved to be Lipschitz stable.
There are some applications to this; Laplace’s equation is used frequently in physics to model
vector fields, especially electromechanical and gravitational fields, as well as for modeling fluids with irrotational flow. In this case, the most pertinent application is for earthquakes- given some readings of the earthquakes magnitude on the surface of the earth, we show that it’s possible, assuming that the crack is linear, to uniquely determine it’s location with some confidence with regard to error. Similarly, after this work is extended to the Helmholtz equation, we could also use it to detect cracks in materials, by placing a regular vibration source on one end of the material and observing the resulting steady state vibrations from a different location on the same side.
The above MQP received an MQP Departmental Honorable Mention for Mathematical Sciences
Title: Stability Properties of a Crack Inverse Problem in Half Space
Student: Andrew Murdza (MA)
Advisor: Darko Volkov
Academic Year: 2019-2020
This project focuses on the analysis of a partial differential equation model relevant in the field of geophysics where sensors can capture seismic and displacement data. The question studied involves whether the geometry of faults, total slip between plates, and accumulated mechanical stress can be determined given data that results in an overdetermined system.
Applied Mathematics
Title: Magnetic Imaging of Current Flow in MXenes Using Quantum Sensors
Students: S. Hanslia and C.E. Williams (MA)
Advisor: Raisa Trubko (PH), Kateryna Kushnir Friedman (PH), Vadim Yakovlev (MA)
Academic Year: 2024-2025
MXenes are a class of low-cost two-dimensional (2D) transition metal carbide, carbonitride, and nitride materials with exceptional electronic, optical, chemical, and mechanical properties. They have high electrical conductivity, offer exceptional strength and stiffness, are biocompatible, and have scalable synthesis methods. As such, they have enormous promise for revolutionizing energy storage, smart textiles, flexible electronics, medicine, 5G/6G communications, ultra-fast sensors, and more. The electrical conductivity of MXenes is influenced by their chemical composition, the configuration of their surface terminations, and the physical MXene geometry. Additives, coatings, or defects in MXenes can be used to tune their electronic properties. It is therefore critical to understand the spatial current flow dynamics in different MXenes. In this work, a combined experimental and computational approach was applied to spatially resolve current flow in MXenes. Quantum sensors was used to image magnetic fields generated from electric current flow through Ti3C2Tx MXenes. Specifically, nitrogen-vacancy (NV) centers in diamond were used to collect vector magnetic field data with micron-scale spatial resolution. A procedure based on the spectral inversion of Biot-Savart law was implemented to reconstruct the current density from the magnetic field. This approach was used to study (i) current flow through pure MXene samples with different geometries and physical defects, (ii) a MXene sample composed with sodium tripolyphosphate (TPP) for stability, and (iii) a MXene sample composed with silk fibroin (SF) for biocompatibility. The data showed that current flowed around physical defects, that the addition of TPP did not fully compromise current flow, and that textured current density was present in the MXene and SF composite material. These results demonstrated a new application for NV diamond magnetometry to study current flow in MXenes. This new robust technique for high-resolution current imaging in MXenes can be used to aid in the future engineering of spatial current-flow dynamics or detection of micrometer-scale defects in MXenes.
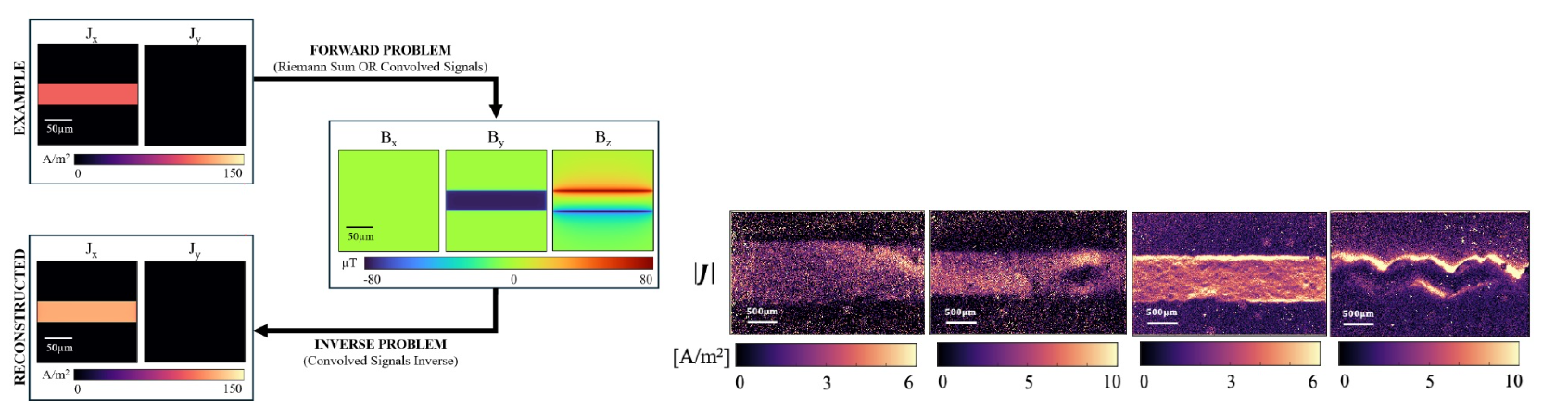
The above MQP won the Provost's MQP Award for Mathematical Sciences 2024-2025
Title: Equivalent resistances in finite and infinite dual graphs
Student: Lil Peeler (MA)
Advisor: Brigitte Servatius (MA), Mostafa Asheghan (ECE)
Academic Year: 2024-2025
The tools of topological graph theory offer insight into the analysis of resistor networks induced by planar graphs and their duals. A study of self-dual maps in particular and their associated resistor networks demonstrates the inherent connection between graph theory and electrical network analysis. In this paper, we define the resistor networks induced by planar graphs, analyze their equivalent resistance properties, and explore self-duality in relation to electrical networks. Finally, we consider the extension of a result concerning the equivalent resistances of finite dual graphs to the infinite case.
The above project received MQP Departmental Honorable Mention for Mathematical Sciences
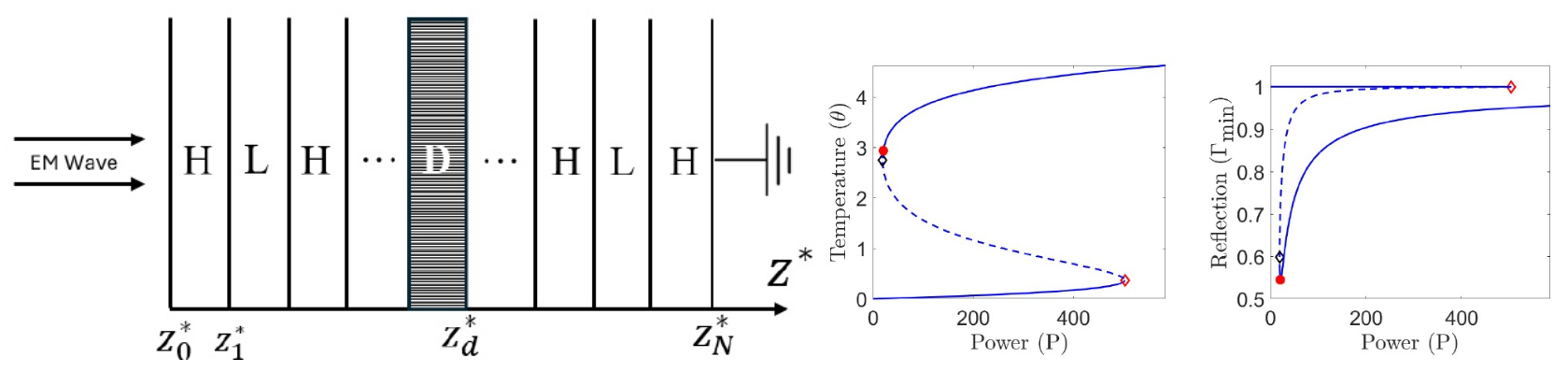
Title: Optimal Defect Layer Position in Electromagnetic Energy Absorbers
Student: Zachary W. Adams (MA)
Advisor: Burt Tilley (MA) and Vadim Yakovlev (MA)
Academic Year: 2024-2025
Beamed energy applications use susceptors to absorb applied electromagnetic radiation and convert it to heat, which can be used to produce useful work. This project considered a susceptor made of a composite material, composed of alternating high and low-permittivity layers. It explored the effects of wave-geometry interactions in this material on energy transmission to the heat exchanger. It was demonstrated that these interactions can be controlled, and reflection at the heat exchanger surface can be minimized by varying only relative layer width and free-space wavenumber. The proposed approach works for both idealized and practical material parameters.
Computational Biomechanics
Title: A Marker-Point Model for Simulation of Elastic Surface Deformation
Student: Kamryn P. Spinelli (MA)
Advisor: Min Wu
Academic Year: 2020-2021
This project developed a higher-accuracy method to simulate the deformation of rotationally-symmetric surfaces such as plant cells. Such a model increases computational efficiency and could be used to better understand how plant cells grow or how deformation can encourage diffusion on the cellular or nuclear level. The project incorporates elements of numerical analysis and differential geometry.
Discrete Mathematics
Title: Tiling of Prime and Composite Kirchhoff Graphs
Student: Jessica Wang (MA)
Advisors: Joseph D. Fehribach (MA)
Academic Year: 2021-2022
A Kirchhoff graph is a connected vector graph (a graph whose edges are vectors) whose cycles are orthogonal to its vertex cuts. For a given matrix, the cycles of a Kirchhoff graph for the matrix form a basis for its null space, while the vertex cuts of the graph lie in its row space. If the Kirchhoff graph is vector 2-connected, then all edge vectors will appear with the same multiplicity. This property is used to develop an exhaustive search algorithm to find all the Kirchhoff graphs for the given matrix up to a certain multiplicity. The algorithm in turn is used to study the structure of families of Kirchhoff graphs, particularly prime, composite and fundamental Kirchhoff graphs. For a given matrix, there are no non-trivial Kirchhoff graphs smaller than a critical multiplicity, and a countable infinite number of prime Kirchhoff graphs whose multiplicity is some multiple of this critical multiplicity.
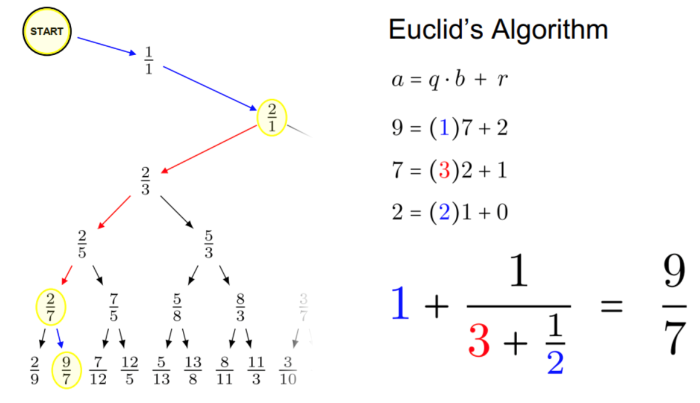
Title: The Calkin-Wilf Tree: Extensions and Applications
Student: Ben Gobler (MA)
Advisors: Brigitte Servatius and Herman Servatius
Academic Year: 2021-2022
Continued fractions are of current interest in mathematics. In a recent publication, Jack E. Graver describes a method for computing terms in the Calkin-Wilf sequence, a list of the positive rationals introduced by Neil Calkin and Herbert S. Wilf in 2000. This paper explores an original method which uses continued fractions to evaluate and locate terms in the Calkin-Wilf sequence, as well as its natural extension to include all of the rational numbers. A generalization of the Calkin-Wilf tree leads to a characterization of rational numbers by continued fractions with integer coefficients. Finally, the meaning of infinite continued fractions and irrational numbers is studied using the structure of the Calkin-Wilf tree. We characterize the irrational numbers which have periodic continued fractions by developing a matrix representation of the setup, and we explain why irrational square root numbers have periodic continued fractions with palindromic coefficients.
Financial Mathematics
Title: Deep Learning for Reflected Backwards Stochastic Differential Equations
Student: Frederick "Forrest" Miller
Advisors: Stephan Sturm
Academic Year: 2022-2023
In this work, we in investigate the theory and numerics of reflected backwards stochastic differential equations (RBSDEs). We review important concepts from stochastic calculus, as well as key theoretical properties of (R)BSDEs. We provide an overview of feedforward neural networks and their applications to functional approximation for numerical implementations. We also discuss the key application of RBSDEs to the field of mathematical finance, in particular indifference pricing of put options. Lastly, we present preliminary theoretical and numerical results of Risk Indifference pricing of American from both the Buyer’s and Seller’s perspectives.
Title: Computations in Option Pricing Engines
Students: Vital Mendonca Filho (MA), Pavee Phongsopa (MA), Nicholas Wotton (MA)
Advisors: Yanhua Li (CS), Qingshuo Song (MA), Gu Wang (MA),
Academic Year: 2019-2020
This project explores how machine learning techniques can be utilized in financial models such as option pricing methods.
Financial Statistics
Title: Analyzing the Dynamic Relationship Between Intraday Trading Activity and Volatility Using High-Frequency Data
Students: Emily Baker (MA), Ryan Candy (MA), Isadora Coughlin (MA)
Advisors: Fangfang Wang (MA), Jian Zou (MA)
Academic Year: 2020-2021
Measuring equity volatility is an important metric and understanding, describing, and predicting volatility using trading activity provides insight into navigating the stock market. Taking inspiration from existing research analyzing volatility in the stock market, we explore the dynamic relationship between trading volume, trading frequency, and volatility on an intraday basis across ten stocks in the consumer discretionary sector of the S&P 100 for the fourth quarter of 2013. Using three different volatility measures we implement variations of the heterogeneous autoregressive model and vector autoregressive model to investigate the lead-and-lag relationship between volatility and trading activity. Our quantitative analysis provides strong empirical evidence that current trading frequency and trading volume can be used to predict 30-minute measures of volatility and that the prior day rolling average and lagged trading measures are useful predictors in modeling the volatility measures.
FinTech
Title: Green Future Wealth Management - Sustainable Investments Return and Risk Expectations
Students: Trajan Espelien (MA/CS), Brandon Lui (CS), Humza Qureshi (DS), Vu Le (CS/DS), Andrew Kovacs (FT)
Advisors: Matthew Ahrens (CS), Marcel Blais (MA/DS), Kwamie Dunbar (BUS), Daniel Treku (BUS/DS)
Sponsor: Green Future Wealth Management
Academic Year: 2024-2025
This project, conducted on behalf of Green Future Wealth Management, focused on developing an application to help investors identify stocks that fit their ESG (Environmental, Social, Governance) values. The team used the Agile Scrum methodology in building the application which features data science to filter the stocks, the Markowitz mathematical framework to manage risk, Tableau to visualize individual company performance, and a JS React & Python Django technology stack. The team successfully integrated investment methodologies and considered investor’s ESG values in recommending an investment portfolio. The project lays a strong foundation for a future integration with the Apex Fintech API to allow for investors to manage real portfolios directly on the platform.
This MQP was awarded the Provost’s Award for Best MQP in Data Science, 2024-2025.
Title: : GraphRAG vs. RAG: A Comparative Evaluation of LLM Performance
Students: Anna Balin (MA/CS), Andrew Cash (CS), Roberto Sabater –(ECE), Inaya Siddiqui (MA), Katie Strogach (CS)
Advisors: Shamsnaz Bhada (ECE), Marcel Blais (MA),Wilson Wong (CS)
Sponsor: A New York-Based Alternative Investment Company
Academic Year: 2024-2025
The increasing complexity of data in alternative investing demands innovative solutions. The industry sponsor currently employs Retrieval-Augmented Generation (RAG) for information retrieval and document ingestion in their AI chatbot. While effective, RAG struggles to answer complex queries requiring synthesis across documents. To address this, we evaluated Microsoft’s GraphRAG, which utilizes knowledge graphs to achieve more sophisticated reasoning and contextually relevant responses. We extensively tested and evaluated RAG and GraphRAG across multiple datasets provided by TPG Angelo Gordon using DeepEval, an open-source LLM evaluation framework. Results were synthesized using Snowflake and SnowSQL and visualized in Power BI.
Machine Learning
Title: Dynamical Systems Approaches for Deep Learning
Student: Neil Kale
Advisor: Randy Paffenroth (MA/CS/DS)
Academic Year: 2023-2024
This study explores iterative neural networks (INNs), which reimagine neural network designs as iterated functions, and the recently introduced Sequential2D framework for neural networks that frames INN functions as left matrix multiplications for enhanced computational efficiency. We investigate the effects of sparse and low-rank matrix approximations on model performance, particularly focusing on sparsity and weight distribution using the MNIST Random Anomaly Task. Our results highlight the delicate balance between parallelization advantages and the need for equitable weight distribution. The comparison of sparse, low-rank, and dense matrices reveals low-rank matrices' role in boosting computational speed without drastically affecting model accuracy. Overall, this research advances our understanding of INNs and Sequential2D, underlining the significance of matrix representation methods in fine-tuning neural network architectures for improved performance and efficiency.
Title: Player Performance Prediction Automation for Draftkings
Students: Kayleigh Cambell (MA), Diego Gonzalez Villalobos (ECE), Benjamin Huang (ECE), Gabriel Katz (MA), Skylar O'Connell (CS)
Advisors: Donald Brown (ECE), Randy Paffenroth (MA)
Sponsor: Draftkings
Academic Year: 2020-2021
In this Major Qualifying Project, we worked with DraftKings, an online daily fantasy sports company, to build a model that would predict the number of points, rebounds, and assists a NBA basketball player would score in a game, as well as the closing lines for NBA games. Our data sources were numerical and categorical data from DraftKings as well as data gathered from third-party sources. Then, we utilized algorithms such as linear regression, Lasso regression, random forest, and neural networks to predict the number of points, rebounds, and assists a NBA basketball player would score in a game, as well as the game lines for NBA games. We were able to reduce the standard deviation of our prediction error substantially for both game lines and for the number of points, rebounds, and assists a NBA basketball player would score in a game.
Mathematical Biology
Title: Parameter Estimation of Cancer Cell Dynamics
Student: Lynne Moore (MA)
Advisors: Andrea Arnold and Sarah Olson
Co-Advisor: Mike Lee (UMass Medical School)
Academic Year: 2019-2020
To screen different drugs as potential cancer therapies, high throughput experiments have been designed to study the dynamics of cell growth and death. Due to experimental costs and limitations, the cell data can only be recorded at a minimal number of time points. In this project, through parameter estimation techniques, we studied the optimal timing of data in order understand time points most relevant to capture cell dynamics.
Probability and Statistics
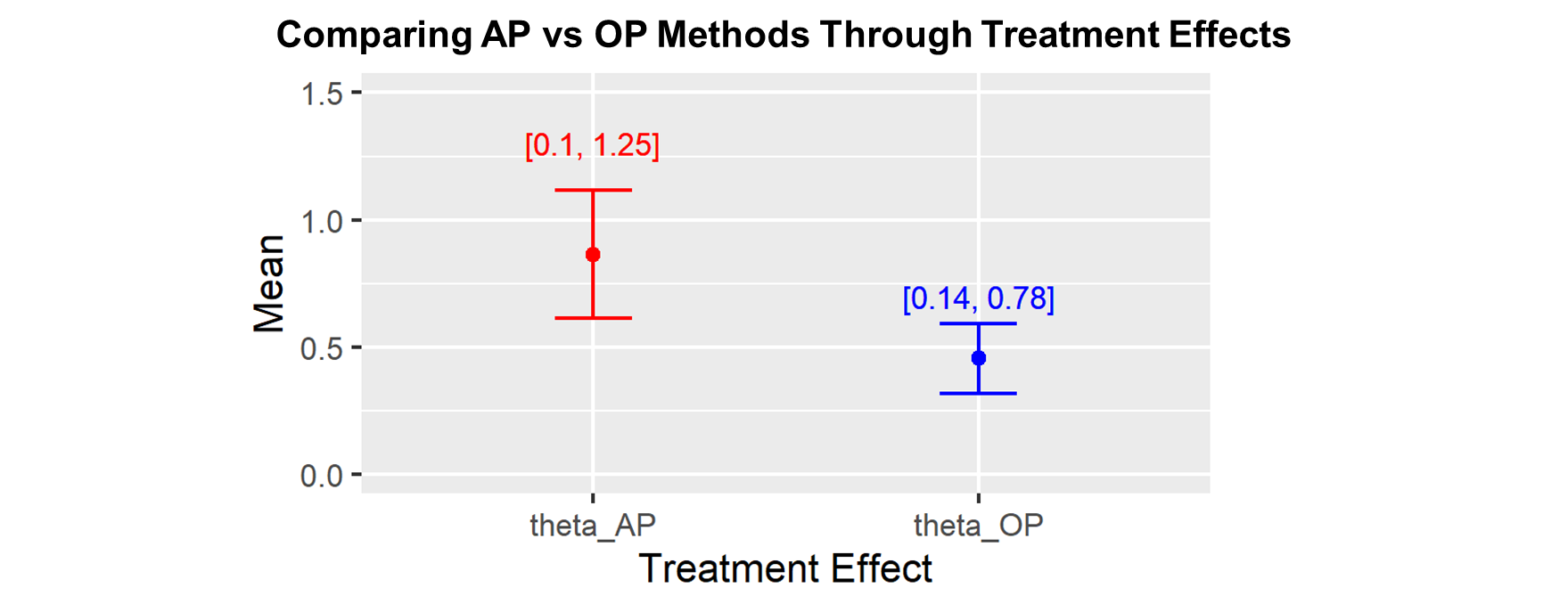
Title: An M-Estimator for the Survivor Average Treatment Effect
Student: Laura Dufresne (MA and SSPS)
Advisor: Adam C. Sales and Alexander D. Smith
Academic Year: 2022-2023
Randomized Controlled trials are considered the gold standard in program effectiveness and other causal research in the social and biomedical sciences because randomizing treatment assignment ensures that subjects in different treatment conditions are otherwise statistically equivalent. However, if some subjects drop out of a randomized study before completion, the remaining subjects may no longer be equivalent across treatment groups. In this study, we developed a novel estimator for the effect of an intervention on the subset of students who would remain in a study regardless of their treatment assignment and applied the method to estimated the effects of an educational technology application from an experiment that took place during the COVID pandemic, which led to missing outcome data for nearly half of participating students.
View additional MQP’s in our project database.
Scientific Computation
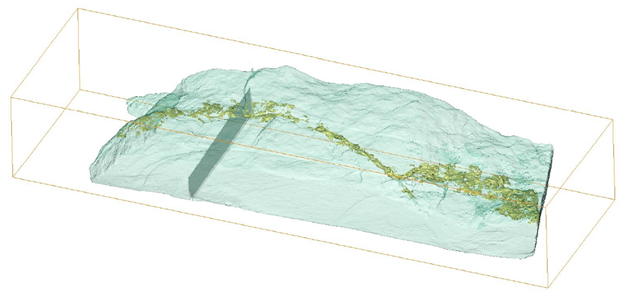
Title: 3D Image Reconstruction of a Fossil Using Neutron Tomography
Students: Agustine Benjamin (PH), Scarlett Clarke (MA)
Advisors: David Medich (PH), Vadim Yakovlev (MA)
Sponsor: Paul Scherrer Institute
Academic Year: 2023-2024
Non-Destructive Testing (NDT) is an interdisciplinary field encompassing various inspection techniques and principles not compromising the structural integrity of the tested objects. Neutron imaging is a very efficient tool of NDT: neutrons, when passing through the sample, are attenuated in accordance with the sample’s composition or geometrical form and produce contrasts made by materials. Neutron computed tomography (NCT) found its use in visualizing the inner structure of industrial, biological, geological, engineering, and other samples of interest. In this MQP, a unique small fossil appearing as the vertebral column of an unknown pre-historic animal embedded in sandstone was investigated with the use of NCT. The fossil was exposed to a neutron beam, and the obtained contrasts were postprocessed with the use of mathematical methods assuming the exponential law of radiation attenuation and using the Radon transform of the distribution of the linear neutron attenuation. A high-resolution 3D image of the sandstone block with the embedded vertebral column was successfully obtained. The image seems to be showing all parts of bones and ribs hidden inside the sandstone block. However, the initial analysis of the image was inconclusive as it was not possible to identify, based on the visible set of bones, the animal behind this fossil. The image, along with the materials documenting the process of image reconstruction, was passed to the owners of the fossil for deeper investigation with the help of paleontologists with relevant expertise.