Designing and prototyping optoelectronic devices can be costly and time-consuming. To mitigate costs, designers use computer software to simulate the operation of the device prior to the construction of a physical prototype. For example, conventional computers can be configured to use mathematical models to represent or approximate an electronic device, such as an electronic package or a multi-layer printed circuit board, and simulate how it will respond during operation.
Certain kinds of electronic devices, such as antennae or integrated circuits, generate electromagnetic fields that can affect their operation. Therefore, to get a complete picture of the how well a device will work, it is important to be able to accurately model those fields, notes L. Ramdas Ram-Mohan, professor of physics and director of the Center for Computational Nanoscience.
“This is a fairly difficult process, but an increasingly important one,” he says. “Very soon, cars are going to be packed with more and more electronics. We may even see that there will be a Moore’s Law for electronics. If so, we may find that we will be reproducing, on a larger scale, what happens when we pack more and more transistors onto integrated circuits. There could be crosstalk. With electronics, we could have electrodynamics crosstalk, which would lead to reduced performance. That is why computer simulations can be of great importance prior to manufacturing of the integrated ‘electromagnetic’ circuits.”
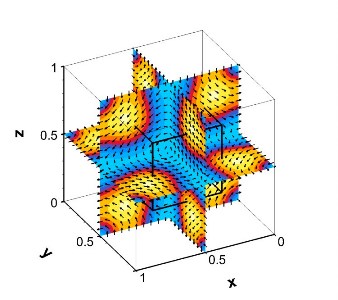
Figure 1: Field patterns displayed in sections of the cube with a dielectric cube embedded in the cubic cavity
To tackle these problems, the WPI research team, including Ram-Mohan, PhD candidate Sathwik Bharadwaj, and Siddhant Pandey, who received a BS in physics and electrical and computer engineering in 2008, in collaboration with colleagues at Michigan State University, developed a node-based Hermite finite element simulation software.
“What we have done,” Ram-Mohan says, “is create improvements in the approach normally taken to model electromagnetic systems. With electromagnetic systems having arbitrary shapes, you would like to be able to employ finite element analysis, but conventional finite element analysis does not satisfy the boundary conditions needed for electrodynamics. So it is better to start off with a different kind of finite elements, Hermite finite elements, which provide greater accuracy with fewer finite elements.”
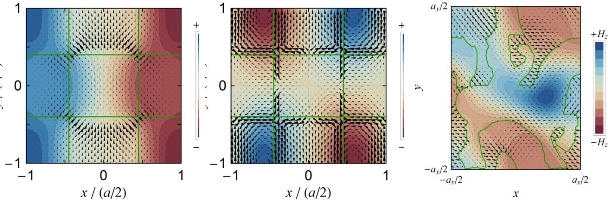
Figure. 2: Electromagnetic field patterns in checkerboard and Escher photonic crystals
Because the new modeling paradigm provides consistency in the direction of fields at the vertices of finite elements, it is well suited to model transport problems such as electron microscope design and particle accelerators, where the particles are driven by microwave fields. The new approach can allow multi-scale calculations with minimal computational costs, which is not feasible within currently prevalent Vector finite element methods, which are used in most of the software packages, due to their lack of unique directionality for fields at shared nodes in the finite element mesh.
The method is shown to produce higher accuracy with lesser computational cost, compared to the electromagnetic simulations implemented in popular software packages such as COMSOL (produced by COMSOL Inc.), HFSS (produced by ANSYS, Inc.), and MFEM (produced by Center for Applied Scientific Computing, LLNL).
“We are increasing accuracy by four orders of magnitude, which is huge,” Ram-Mohan says. “This means we need many fewer elements than any other scheme.”
These findings were published in the following articles in the Journal of Applied Physics:
1. Cavity electrodynamics with Hermite interpolation: Role of symmetry and degeneracies, Siddhant Pandey, Sathwik Bharadwaj, M. Santia, M. Hodek, J. D. Albrecht, and L. R. Ram-Mohan, Journal of Applied Physics 124, 213106 (2018).
2. Hermite finite elements for high accuracy electromagnetic field calculations: A case study of homogeneous and inhomogeneous waveguides, C. R Boucher, Zehao Li, C. I Ahheng, J. D. Albrecht, L. R. Ram-Mohan, Journal of Applied Physics 119, 143106 (2016).
3. Efficient Modeling of Photonic Crystals With Local Hermite Polynomials, C. R. Boucher, Z. Li, J. D. Albrecht, L. R. Ram-Mohan, Journal of Applied Physics 115, 1-10 (2014).