Euler’s Number: A Way to Celebrate Our Nerdy Side

In the American notation for dates, February 7 is 2/7/18. That’s cool, because a fundamental mathematical constant, sometimes called “Euler’s number”—named for 18th Century Swiss mathematician Leonhard Euler—is e = 2.718. Well, not exactly: e goes on forever without repeating itself. We call that irrational. The beginning of the song sounds something like this:

e = 2.71828182845904523536028747135266249775724709369995957496696762772 …

In fact, the number e is transcendental! To get it exactly, one might add up

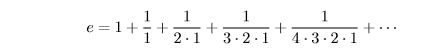
…but that would take forever!

Bill Martin using e to chart how the stock market has

performed over a 50-year span.

Before we get to the mystery of e, why do we associate dates with math anyway? Well, because it’s fun. It gives us a way to celebrate our nerdy side without getting in too deep. Each year we celebrate “Pi Day” (March 14) because, for any perfect circle the circumference divided by the diameter is 3.14159265358979323846264338327950288419716939937510 . . . or thereabout.

Others celebrate “Tau Day” 6/28, “Fibonacci Day” 11/23, “Mole Day” 10/23 (at 6:02 a.m., of course), and so on. Pythagorean Triple Days come much less frequently: the most recent one was 8/15/17 and the next will be 12/16/20.

Then there are once-in-a-lifetime dates, like the most recent “Odd Day” 11/29/1999. But many coincidences are a lot less rare than we might think. Friday the Thirteenth had better not be unlucky: it happens to us almost twice a year. (Why? If the 13th of the month were to land on a day of the week uniformly at random, then one in seven of them would be Fridays.) Our brains are wired to see patterns in numbers and the calendar and the clock offer numbers to us every day. We can’t resist.

Technical professionals use ‘e’ as the common base for growth rates, ranging from financial investment to rate of spread of disease. So, in that sense, the number ‘e’ is central to most fields of science and engineering.

One of the applications of the number ‘e’ is in financial and economic modeling. It allows us to understand longterm behavior.

In fact, if you look at the Dow Jones Industrial Average over the past two weeks, you won’t see any pattern. It looks like total randomness. However, when you look at the Dow Jones over the past half century, you’ll something very close to an exponential function. And these functions are always written using Euler’s number ‘e.’

Now there are many ways to approach this number Euler gave us. We could talk about sums of fractions or calculus with exponential functions. But perhaps the most memorable way to play with e is to consider compound interest. Suppose, at noon on February 6, you give me one hundred dollars because I have promised to double it in one day. Yes, I’m feeling generous and so I will offer you 100 percent simple interest in just 24 hours. You can give me $100 and get $200 at exactly noon on February 7.

You ask me: “If I instead cash out at midnight, shouldn’t I get 50 percent interest for the half-day?” I might respond, “Sure, at midnight, I’d give you $150.” But you are smart and you then say, “And if I re-invest that $150 from midnight ‘til noon the next day, shouldn’t I be entitled to 50 percent interest on that half-day investment?” Somehow I’m not paying careful attention and I reply, “Sure,” having just committed to giving you $225 (that’s (1.5) × $150) instead of the $200 I originally promised.

You continue in this manner. Cashing out and re-investing every six hours gets you (about) $244.14 (net proﬁt $144.14 after you account for your original $100). A transaction per hour leaves you with a handsome sum of $266.37. And so on. You might start to think you can make millions of dollars off of my 100 percent interest promise if you just divide the day up into enough pieces.

If you cash out and reinvest every minute, you end up with $271.73 at noon on Feb. 7; every second leads to $271.82 ... (a gain of $171.82). And now you see that you are running up against a wall: even if you could program a computer to compound the interest every microsecond (there are a million of these per second, so that would have to be an amazing computer with an incredibly fast connection), you would still end up with just $271.82 (and 0.81828443314437742057 … cents).

But, hey, you’re getting 100 percent interest, and it's compounded so frequently that you’re getting $171.82 in total interest on 2/7/18. So, at noon on “e Day” you’ll still be a happy camper. Just be glad you’re not one of those people stuck paying interest at a rate of 30 percent or so compounded monthly on some deceptively marketed credit card!

- By William Martin

Professor of Mathematical Sciences