Research

Mathematical Sciences Research Seminars

The WPI Mathematical Sciences Department hosts several research seminar series. We invite you to take a look at what seminars are currently scheduled. For further information regarding Mathematical Sciences seminars please contact the main office at 508-831-5241 or ma-questions@wpi.edu.

Scheduled Research Seminars

The Mathematical Sciences faculty members are currently involved in a wealth of diverse research projects, both fundamental and applied:

Algebra/Discrete Mathematics

Fehribach, J., Humi, M., Martin , W., Servatius, B., Tripp, S., Wagner, A.
Post-Doctoral Scholars: Uricchio, N.

Cryptography
Discrete Geometry
Graph Theory and Combinatorics
Group Theory
Linear Algebra
Matroids
Symmetry and Lie Groups

Analysis

Fehribach , J., Larsen , C., Lurie , K., Peng, G., Vernescu, B., Volkov, D.
Post-Doctoral Scholars: Buczkowski, N.

Calculus of Variations
Nonlocal Models
Partial Differential Equations

Applied Mathematics

Arnold, A., Bernardi, F., Blais , M., Fehribach , J., Humi, M., Larsen , C.,Lurie , K., Nachbin, A., Olson , S., Peng, G., Sarkis , M., Servatius, B., Song, Q., Sturm , S., Tang , D., Tilley , B., Wang , F., Vernescu , B., Volkov, D., Wagner, A., Walcott, S., Wu, M., Zhang , Z.
Post-Doctoral Scholars: Ashenafi, Y., Buczkowski, N., Zhuang, Q.

Fluids
- Computational Biofluid
- Energy-Fluid-Chemical Transport Through Porous Media
- Interfacial Phenomena of Fluid Mechanics
- Microfluidics
- Water Waves
Mathematical Biology
- Biomechanics
- Computational Bioengineering
- Image-Based Modeling for Vulnerable Plaques
- Image-Based Ventricle Models
Mathematics of Materials Science
- Defect Evolution
- Defect Structure
- Dynamic Materials
- Geothermal Energy Harvesting
- Optimal Material Design
- Porous Electrodes
- Soft Biological Tissue
Mathematical Physics
Numerical Analysis/Computational Modeling
- Domain Decomposition
- Finite Element Methods
- Numerical Methods
- Scientific Computing
Probability and Stochastic Analysis

Financial Mathematics

Blais, M., Song, Q., Sturm, S., Wang, F., Wang, G., Zhang, Z.

Computational Finance
Mean Field Games
Option Pricing and Hedging
Portfolio Selection and Investment
Systemic Risk

Statistics

Nandram, B., Paffenroth, R., Peiris, B., Sales, A., Wang, F., Wu , Z., Zou, J.

Biostatistics and Bioinformatics
Biosurveillance and Spatio-temporal Statistics
Compressed Sensing
Causal Inference
Network Analysis
Time series and Financial Statistics
Unsupervised Machine Learning

Predicting Cracks in Materials

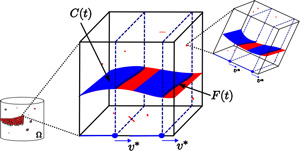
Christopher Larsen studies applied analysis and materials science. Currently, he is captivated by research in the field of fracture mechanics, particularly predicting crack sets in physical materials.

Breathing New Life into Materials

Having pioneered the field of optimal material design, Konstantin Lurie is shaking up the materials world again. He wants the world to begin to think of materials in a new way. Instead of substances with constant properties, he has shown that materials can be entities whose properties can change—in space as well as time.

Computational Biology

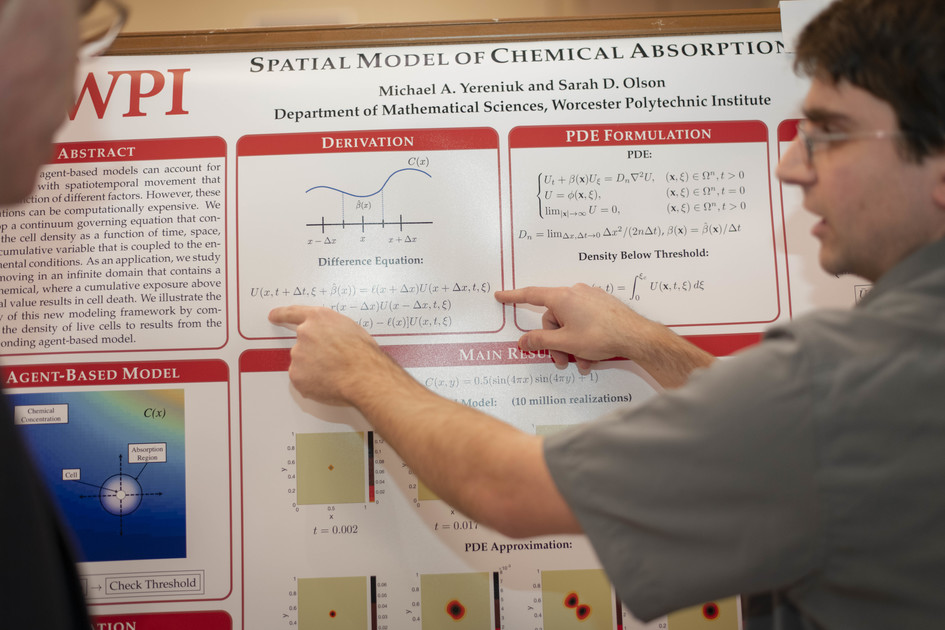
Modeling frameworks can be utilized to understand, predict, and control many biophysical processes. Sarah Olson works at the intersection of Applied and Computational Mathematics to develop, analyze, and simulate new models to test hypotheses and understand emergent phenomena in biological systems.

Machine Learning

Machine learning impacts may aspects of our lives, from shopping and social media to AI assistants and gaming, but the mathematical theory of many such algorithms is not well understood. Randy Paffenroth works at the intersection of Mathematical Sciences, Computer Science, and Data Science to better understand and improve these ubiquitous algorithms.

Using Matroid and Graph Theory for Diverse Applications

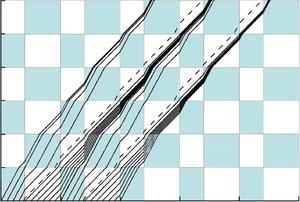
Brigitte Servatius is a discrete, or finite, mathematician, and her major tools are matroid and graph theory. Matroid theory is essential in developing and speeding up algorithms that are used to power the Internet and implement GPS tracking technology, among other applications.